A Gentle Introduction to the Rendering Equation
August 11, 2022
I’ve been playing around with Blender lately, and it’s amazing how software can produce incredibly realistic images from 3D scenes.
Notice the effects in the image below.
The ripples in the water, smoke coming out of the chimney, the glow from the fireplace in the cabin. All of these are computer-generated.
 Lake House by kless, made with Blender.
Lake House by kless, made with Blender.Blender has a powerful built-in renderer called Cycles that produced this image. The artist created the 3D models, specified their materials, added some details and lighting, and Cycles generated the 2D image.
What if you wanted to write your own renderer?
You'd need to first model the way that light moves in 3D space. You'd need a rendering equation.
The equation above is the Rendering Equation, which calculates the light leaving a point on an object in a certain direction.
We'll first get a feel for how this works, and then go over it in detail.
Why is the wall orange?
Let's take a deeper look at one spot on the image above: the glow from the fireplace on the interior wall.
 A spot on the interior wall.
A spot on the interior wall.Here we have a 3D scene that includes just the two walls of the cabin and the fireplace.
 A simplified recreation of the walls of the cabin and the fireplace.
A simplified recreation of the walls of the cabin and the fireplace.Imagine a beam shooting out from the bright fire in the fireplace, bouncing off the wall, and hitting our eye.
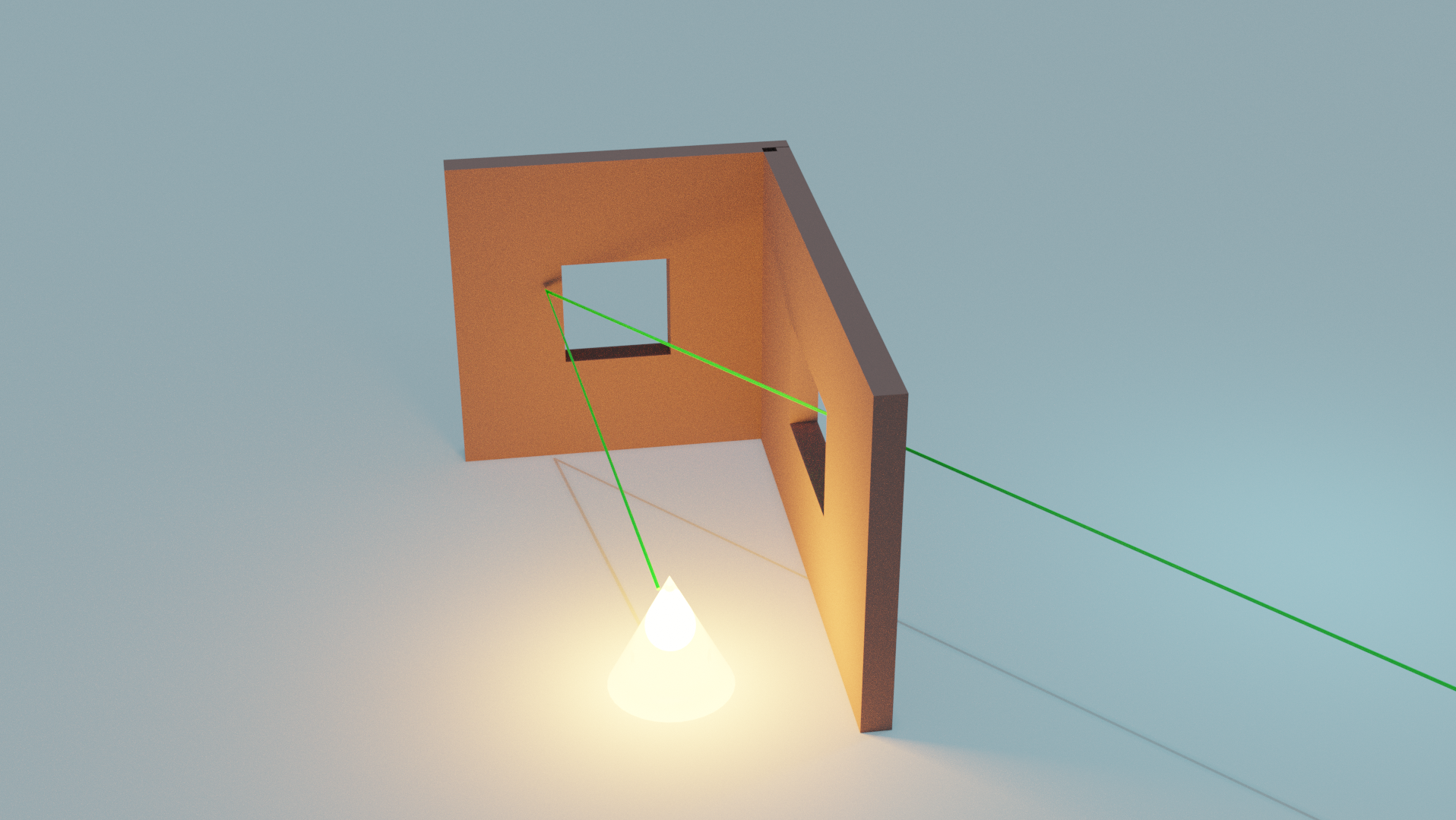 The green line shows the path the light ray takes from the fireplace to our eye.
The green line shows the path the light ray takes from the fireplace to our eye.The yellow light of the fire travels to the wall, mixes with the brown wood, and a portion of it bounces back toward our eye to give us an orange colour.
The Rendering Equation tells us exactly how the properties of the wall, the fire, and the angles of the bounces combine to give us this colour.
Building some intuition
Let’s go over some concepts that can help you intuitively grasp the Rendering Equation.
How light can hit your eye
There are three ways that light can hit your eye:
- Light directly hits your eye: the light from a lightbulb 💡
- Light refracts: the sun shining through a glass window 🪟
- Light reflects: the sun reflecting off of a car 🚙
Everything reflects
When we think of reflecting, we often think mirrors, but every object reflects light to some degree. If you’re reading a book on a sunny day, you’re reflecting a little bit of light onto your face.
Material matters
Imagine you're holding a mirror in your hands angled towards your face on a sunny day. This is going to shine a lot more light onto your face than if you were reading a book.
Materials affect the light that's reflected off a surface.
The equation
Okay, now onto the equation.
This calculates the outgoing light from a point on a surface.
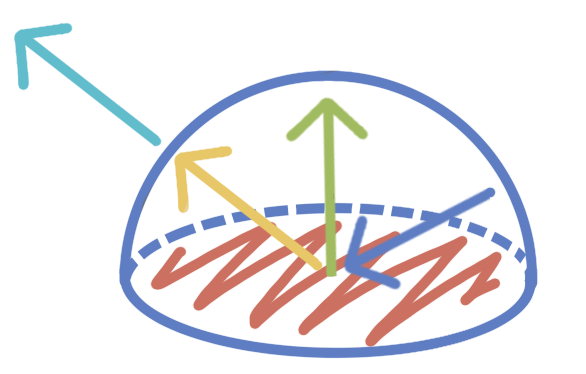
Put more simply: the light that hits your eye = the light emitted from the object + light hitting the surface from every 3D direction weighted by some calculations having to do with the material and the angle.
Light hitting your eye
This is what we're calculating, the light from a point on a surface in the direction toward your eye.
Light emitted from the object
An object itself can emit light, like a fire, or a piece of metal that gets really hot.
Incoming light
When we think of light bouncing, we might think it comes in at the same direction that it leaves, like a mirror. But for any realistic surface, there are many light beams that will exit in a different angle.
This means the light reflected from a surface into our eye could have hit the surface at any angle. So, to account for all this light, we have to consider every incoming direction.
The material function
The material function considers many properties of the material and how they affect how the incoming light reflects into outgoing light.
Materials (like metal and paper) have different properties that affect how light is reflected and refracted. A mirror might reflect a lot of light, with the same colour as the incoming light.
Properties include roughness, transmission (high for glass), and specularity (low for matte surfaces).
The dot product
The difference between the surface normal and the angle of the incoming light affects how much light is reflected.
If the incoming light angle is close to the normal, the amount of light will be higher.
Back to the orange spot
Now that we have an understanding of how the Rendering Equation works, we can look at the interior wall example again.

Light hitting your eye
We're calculating the light from the spot on the wall to our eye.
Light emitted from the object
The wall itself doesn't emit any light. The fire emits light, which increases the amount of incoming light onto the wall.
Incoming light
We have the strong warm-coloured incoming light from the fire, as well as light bouncing off the surrounding walls to hit this one spot.
The material function
The brown wood stain on the wall absorbs some light wavelengths and reflects other wavelengths, which gives the reflected light a more brown tinge. The wood is rough, so it doesn't always reflect light at a mirrored angle.
The dot product
The wall is directly facing the fire, so it receives a lot of its light.
The result
And our final colour is a fairly bright orange from the strong yellow light mixing with the brown stain on the wooden wall.
Questions
How is colour represented in this equation?
We've been talking about how the rendering equation measures "light." More specifically, what it measures is something called spectral radiance. Put simply, spectral radiance is a representation of light that encodes data that gives us the colour and intensity.
What about refraction?
The equation above just focuses on reflection, but can be expanded to include refraction. Instead of integrating over the unit hemisphere, we'd integrate over the unit sphere, and the material function would account for transmission of light.
What other techniques do renderers implement to solve the rendering equation?
Renderers may sample a pixel many times to produce the most accurate colour, ignore objects that are far away, and use integrated hardware like GPUs to speed things up.